A little joke on a regular day

[NX-01]

[ishaan2479]

@Kresimir

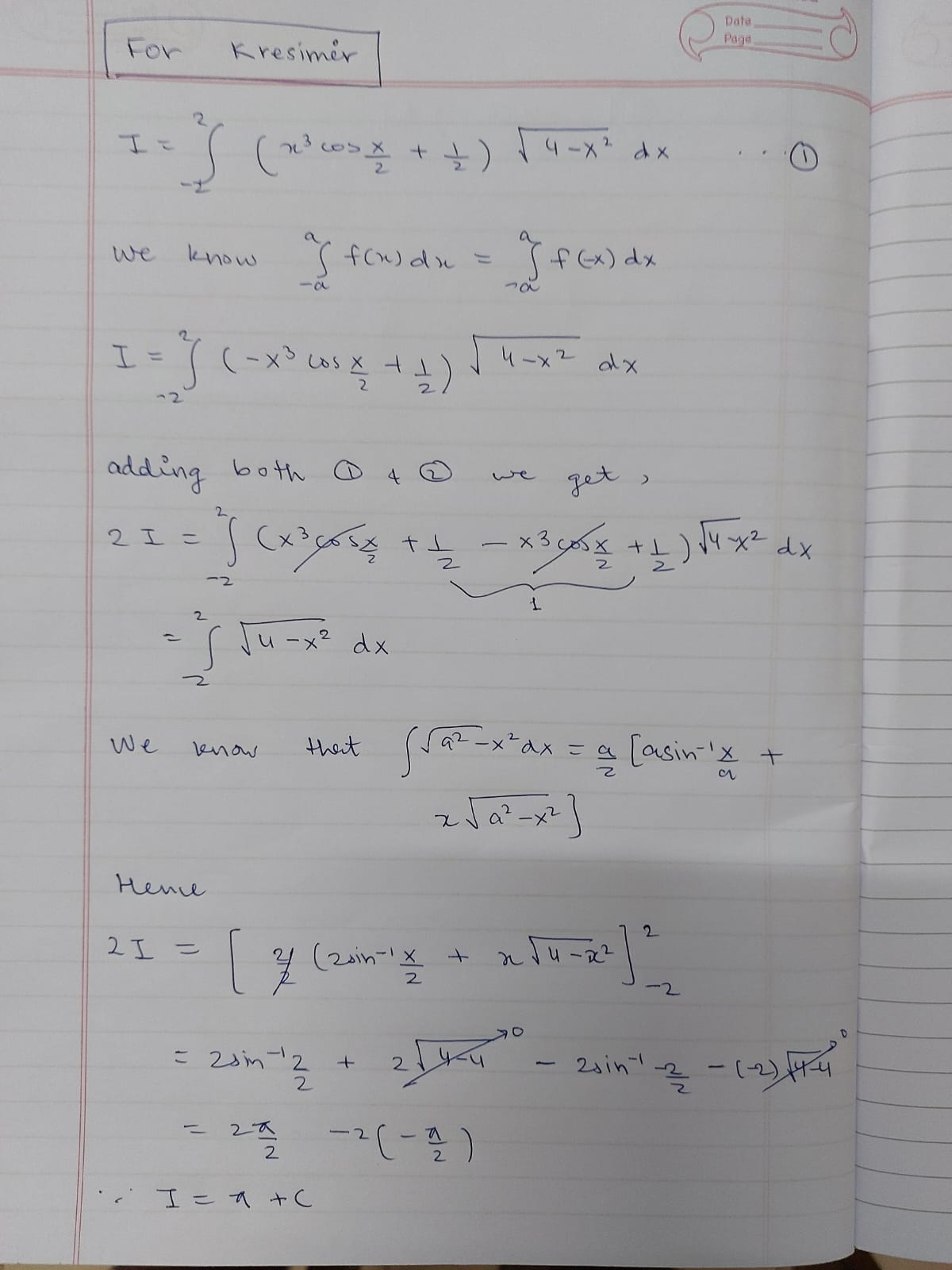
Answer would be first 10 digits of pi (what about the C though?)

---

Alternate approach with python:

sudo pacman -S python-sympy
python main.py

# main.py
from sympy import *

x = Symbol("x")
expr = (x**3*cos(x/2)+(1/2))*((4-x**2)**(1/2))
res = Integral(expr, (x, -2, 2)).evalf()
print(res)

first_10_digits = int(str(res).replace(".", "")[:10])
print(first_10_digits)

[SearingSunrazeSmash]

I would have used SageMath.

[sradjoker]

@ishaan2479

Answer would be first 10 digits of pi (what about the C though?)

This means that:

@Kresimir

it’s a fairly easy problem that one solve without a pen and paper

Its not easy to solve without pen and paper.

[Kresimir]

@ishaan2479

(what about the C though?)

There’s no C, it’s a definite integral. You should not just mechanically write + C at the end, but understand where that C is coming from.

When you have an indefinite integral (the antiderivative) then you have to add C because dC/dx is zero, so all functions that differ by a constant have the same derivative. But when you have a definite integral, then from Newton-Leibniz formula you have a difference of antiderivatives at the endpoints of the interval, so C and −C cancel out.

@sradjoker

Its not easy to solve without pen and paper.

Yeah it is. It’s actually super simple, once you see it. You don’t have to do any integration at all.

What you have to notice is that the first term in the parenthesis is zero (definite integral of an odd function over a symmetric interval is always zero). That part is merely a sneaky diversion made to confuse you…

So now you only have the integral of sqrt(4 − x²), from −2 to 2, which you should recognise as the half of the area of a circle with a radius 2, and that’s 2π, which you halve again (factor 1/2 in the parenthesis) to get the final answer: π.

[sradjoker]

@Kresimir

You have to notice that the first term in the parenthesis is zero (definite integral of an odd function over a symmetric interval is always zero). That part is merely a sneaky diversion made to confuse you…

I was able to notice the first term was zero. Also, it been a while so I didn’t know that term was area of a circle. But now I recall. Finally I don’t know first 10 digits for pi though.
Let me try:
3.14159
So I remember 5 digits

[33Nicolas]

[pebcak]

[SearingSunrazeSmash]

@Kresimir

So now you only have the integral of sqrt(4 − x²), from −2 to 2, which you should recognise as the half of the area of a circle with a radius 2

Sorry for joining in late. When you were active over this, I went to sleep as it was 11 PM.

My question is, how did you identified that this expression represents semicircle ?
Though, the presence of squared terms inside sqrt feels related to that.
As this expression is even function, then its integral should be twice of function from 0 to 2, which will cancel out the remaining half.

My approach to solve the question was to analyze the even-odd functions as the integrand is subjected to same limit with opposite sign.




Also, the 2π term or terms related to π often comes in Cauchy Integrals and related topics, therefore, can this question be approached by this method ? But I doubt over this as the quoted expression can’t be assembled to required form for CIF.

[Kresimir]

@SearingSunrazeSmash

My question is, how did you identified that this expression represents semicircle ?

I know the circle equation in the explicit form:

y = ± sqrt(R² − x²)

The + sign is for the upper semicircle, and the − sign is for the lower semicircle.

I don’t know what they teach in India, but here in Croatia, this is the first grade of high school or something like that. Every 14 or 15-year-old should know this.

But if you don’t know it, just remember the definition of a circle: a set of all points at a given distance from its centre. And if the centre is (0, 0) then this set of points in the Cartesian coordinates (x, y) is given by the Pythagorean theorem:

x² + y² = R²

This is the so-called implicit circle equation. Just solve for y and there you have it.

So, when you identify it as a circle, you don’t need to solve an integral, you already know what the area of a circle is. That’s why this problem is so easy, if you see the trick.

[33Nicolas]

[33Nicolas]

When I traveled often, I would shoot pictures of toilets abroad. This one isn’t my shot, but it’s a fine specimen of some of the wild toilets you find out there.

[Kresimir]

@33Nicolas

but it’s a fine specimen of some of the wild toilets you find out there.

It’s a fine specimen of “flip image horizontally” in any image editing tool.

[SearingSunrazeSmash]

Okay.

I was aware of this. This was taught to us when I was in class 8th. Just had never used the explicit form in past couple of years, hence it didn’t clicked.

I was thinking something else, related to CIF.

[RokettoPanchi]

[djwyman]

When I was in the Army I found that some middle eastern bathrooms would just have a floor with a hole in it…it was kinda weird but then they also had gold toilets in the same area so it was kinda weird.

[Talera]

[joekamprad]

it is a … little joke on a regular day ?

[33Nicolas]

I don’t understand what you wrote. Is it flipped for you? It isn’t for me on displaying flipped.

[Kresimir]

The image was created by deleting half of it and mirroring the other half.

Like this: